車の「最小回転半径」
この記事をシェア

文と構成=横内 信弘 写真と動画=勝尾 仁
こんにちは、ライターの横内です。車の「最小回転半径」ってご存知ですか? これは、車のカタログに載っている、「小回り」のよさの目安になる数値のことです。
めいっぱいハンドルを切って旋回した時に一番外側のタイヤの中心が描く円の軌跡。この円の半径を「最小回転半径」といいます。
今回の実験では、JAF新井インストラクターと一緒に、この最小回転半径を実測してみたいと思います!
新井インストラクター、よろしくお願いしま~す。
カーメーカーに教わりました。
最小回転半径には、算出するための計算式があった!
ところで、カタログに記載されている最小回転半径の数値は、カーメーカーさんではどのように計っているのでしょうか? 私たちのように、実測しているのでしょうか?
そこで、実際にカーメーカーさんに話を聞いてみました。
すると、「すべて理論値です」とのこと。
「最小回転半径に関して保安基準に記載があり、それにのっとって計算により求めています」(カーメーカー広報担当者談)
なるほど~そうなんですね。
保安基準とは、「道路運送車両の保安基準」のことで、道路運送車両法という国の法律があって、その細かい部分を定める省令にあたります。ちなみに、道路運送車両法には、道路運送車両法施行令という政令、道路運送車両法施行規則という省令もあります。
そこで、この保安基準を調べて計算式を確認してみたのですが、こんな感じでした。

ハァ─・・・。若かりし頃に見聞きした「sin」や「tan」をはじめ、それらがルート(√)の中に入っていたりで、頭の中は大混乱です。拒絶反応が起こる中、それでも何とか保安基準の該当ページを読み進めてみて、私でも確認できた情報を以下にご紹介します。
まず、計算式に使われている記号の意味ですが、以下のようになります。
R:最小回転半径
L:軸距
Tf:かじ取り車輪の輪距
α:外側車輪のかじ取り角度
β:内側車輪のかじ取り角度
「軸距」とは、前軸と後軸の間の距離で、ホイールベースのこと。「かじ取り車輪の輪距」とは、通常の乗用車では、左前輪の中心から、右前輪の中心までの距離で、いわゆるトレッドベースのことです。
また、保安基準では、最小回転半径についての説明は次のようになっています。
「かじ取装置を右又は左に最大に操作して低速で旋回させた場合の外側タイヤの接地部中心の軌跡の最大半径」
最小回転半径には、ハンドルのかじ取り角度以外にも車の大きさはもちろん、タイヤの位置、車の速さまで関係があるみたいですね。
カーメーカーさんは、次のようなことも教えてくれました。
「たとえ実際に走行して最小回転半径を測っても、カタログに載っている理論値と同じ数値になることはありません。なぜなら、路面の状況(水平角度、滑りやすさ)、タイヤの状況(純正かどうか、減り具合)、ハンドルの切り具合など、不確定要素が大変多いからです」(カーメーカー広報担当者談)
こうは言われたものの、保安基準の計算式ではまったく理解できないので、私たちには理論値を計算してみることもできません・・・。
なので、実際に車を旋回させて最小回転半径の円を描き、そこから中心を見つけ出しその半径を実測してみたいと思います!
→次ページ:まずは、ハンドルをめいっぱい切って車で円を描いてみた。

今回、最小回転半径を実測するのは、写真の赤いコンパクトカー。カタログによるとこの車の最小回転半径は「4.7m」とあります。
この車にエジソンスタッフが乗り込み、左にめいっぱいハンドルを切り、保安基準にあった「低速」(徐行)で旋回を始めます! この時に、運転席側の前輪タイヤの外側にもう一人のエジソンスタッフがスタンバイし、ぴったりチョークを押し当てタイヤの外側の軌跡を描いていきます。
保安基準では、「タイヤの接地部中心」とありましたが、これは現実的には計測が難しいので、今回は「タイヤの外側の軌跡」を計測することにしました。

徐行する車に、必死にチョークを押し当てるエジソンスタッフ。アスファルトの路面が微妙にボコボコしており、きれいに描くのに大変苦労している様子でした。上手くいけば、直径約10mの大きくてきれいな円になるはずです!
ただ、そもそも一周してちゃんと円になるのかどうか疑問でもあります。
そんな不安と期待を抱きながら、計測は始まりました!
ちなみに計測の様子は、高所作業車(ハイライダー)からも撮影。真上から見て、キレイな円になっているかしっかり確認します。

円が描き終わりました。結構きれいな正円で描けました! 実験は大成功、バンザーイ。
いえいえ、これから、半径を計測するんでした・・・。半径を計測するためには、円の中心がどこなのかが分からなければなりません。
さて、円の中心の求め方。どのように求めるか皆さん覚えていますか? そう、コンパスを使って求めるアレです。学校で習いましたよね?
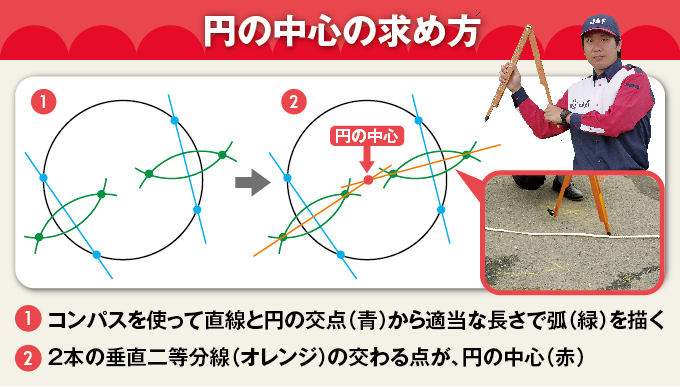
円の中心が分かりました! ここから半径を計測してみると4.9mあります。あれ、カタログに記載されていた最小回転半径4.7mより長くなってしまいました・・・。
どうしましょう、新井インストラクター?
「カタログの数値は、タイヤの接地面の中心からの理論値です。今回の計測はタイヤの外側の軌跡を描きそこからの実測値なので、このくらいの誤差が生じてもやむを得ないと思います」(新井インストラクター談)。
たしかに、そうでした! もしかして、結構な精度で円が描けているんじゃないでしょうか?!
あれ、でもちょっと待ってください。
そういえばこの円の中心、車に対して随分後ろにあるんですね。何というか、思っていたイメージと違うというか・・・。
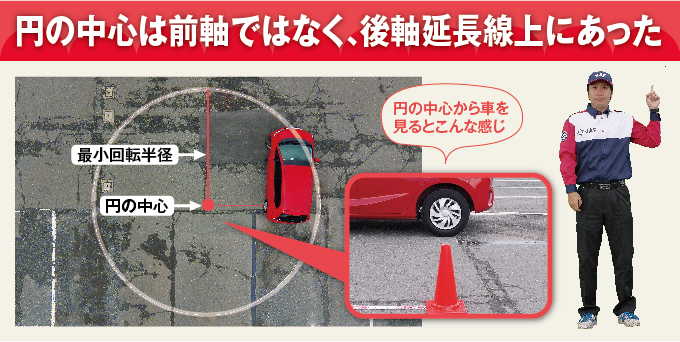
「実は最小回転半径の中心は、常に2つの後輪の中心を通る直線上に位置しているんですよ」と新井インストラクターは話します。
それって、すなわちどういうことなんでしょうか??
→次ページ:円の中心が後軸の延長線上にあると、円はこう描かれる。

円の中心が運転席よりずいぶん後ろにあることに、なんだか違和感がありますね・・・。
この違和感は、一体何なのでしょう??
新井さんによると、実はこの点が、最小回転半径を正しく理解するうえで重要なポイントだと言います。
「例えば、今回の『最小回転半径4.7m』の車の正面に壁があるとします。そして、その壁に当たらないようにめいっぱいハンドルを切って(フルロックで)、写真のように左折するとしましょう。すると、この壁と停車している車の先端との間に必要な距離は、4.7mよりもずっと短い長さで十分なんです(最小回転半径の円の外側になる右フェンダー部分を差し引いたとしても十分短い)。下の図のように、正しい最小回転半径のイメージと間違った最小回転半径のイメージを比較すると、分かりやすいですよ」(新井インストラクター談)
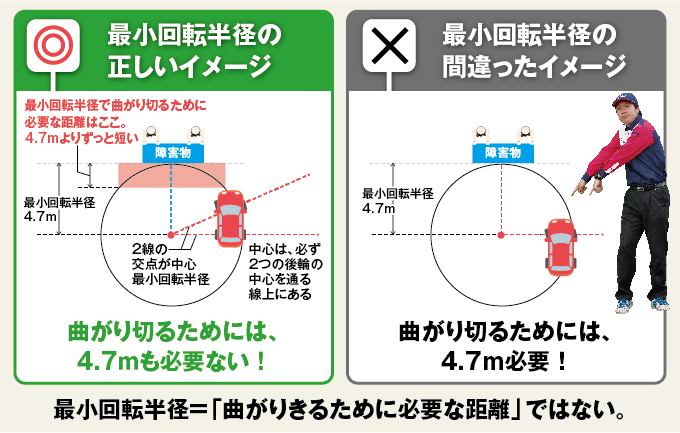
なるほど! こういうことだったんですね。
「小回りの良さ」って、つい運転席(前輪)を中心にイメージしてしまいがち。その目安となる最小回転半径も、当然運転席(前輪)が基準になるものだと思い込んでいました・・・。
でも、本当はそうではなく、最小回転半径の円の中心は、後輪(後軸)の延長線上にある。だから、壁までの距離4.7mの中に、すでに車の大半が含まれてしまっているんですね。
円の中心の位置が分かった時に抱いた違和感は、横内の思い込みとの差異によるものだったというわけです。
→次ページ:正面の壁を曲がり切る場合とUターンする場合の違いとは?

新井インストラクター、最小回転半径の秘密がだんだん分かってきました!
そこで、仮定の話になりますが、ちょっと教えてほしいことがあります。
今回実験で使用した車は、最小回転半径が4.7mのコンパクトカーでしたが、これが仮にもっと大きい場合、例えば1m伸びて5.7mになると、車の動きはどのようになるのでしょうか?
「それでは最小回転半径が4.7mの車と、仮に最小回転半径が1m伸びて5.7mの2台の車が同じ場所からフルロックで今回のように旋回するとします。すると、円を描く一番外側の前輪がそれぞれ時計の12時の位置に到達した段階で、2台の車の最小回転半径には1mの差がついています。最小回転半径が5.7mの車では、今回の壁にぶつからずに曲がりきることはできませんね」(新井インストラクター談)
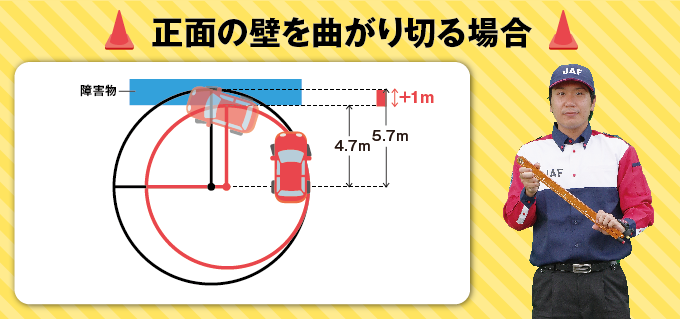
「車が壁の前を通り過ぎてそのまま旋回を続け、反転した状態(Uターンの状態)では、さらに差が開き、最小回転半径4.7mの車と5.7mの車とでは、2mもの差がついてしまうんです。図で示すと以下のようになります」(新井インストラクター談)
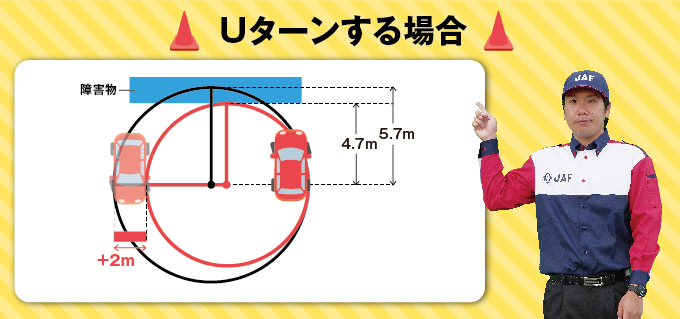
なるほど~最小回転半径が大きくなると、車の動きにはこのように影響するんですね。
ドライバーのみなさんへ。
最小回転半径を理解して安全運転をお願いします。

「ドライバーの皆さんは、今回を機会にマイカーのカタログや取り扱い説明書に記載されている最小回転半径をチェックしてみてはどうでしょうか? 特に車の買い替え時や会社の車に乗り換える時などは注意が必要です。普段乗っている車より、最小回転半径が仮に1m伸びていると、正面の障害物を曲がりきるためには+1mの距離の感覚が必要になり、さらにUターンをする場合には+2m、倍の距離感覚が必要になります。また、最小回転半径はあくまで前輪タイヤの接地面の中心からの距離です。その一回り外側には、いつもフェンダー部分が出ていることにも注意してください」


























